Rodrigo Strauss :: Blog

Tutorial de STL, parte 1/2: Mais templates

No primeiro post da série vimos qual a função básica dos templates: transformar os tipos de dados em parâmetros, assim como já são os valores. Isso permite que você faça uma função - na realidade um template de função - que consiga tratar vários tipos de dados e continuar tipada. Essa é a base do "generic programming", separar o algoritmo do tipo de dado. Dessa forma, qualquer tipo de dado que tenha suporte aos requisitos exigidos para o funcionamento do algoritmo pode ser usado. Esses requisitos em relação a um tipo de dado tem o nome de "concept", e será nativamente suportado pela linguagem no C++0x. Veremos mais sobre isso em breve.

No nosso primeiro exemplo resolvemos o problema de duplicação do código da função, mas não resolvemos o problema do código que chama a função, pois só trocamos a sintaxe soma_int para sintaxe soma<int>. O que eu não contei na primeira parte é que o compilador C++ faz a resolução automática de tipos para os parâmetros, sempre que possível. Nosso código pode ser modificado para:

template <typename T>
T soma(T x, T y)
{
  return x + y;
}

int main()
{
  soma(2,2);
  soma(2.99f, 2.99f);
  soma(5.9999, 6.9999);
  soma('2', '2'); // não, o resultado não será '4'...

  return 0;
}

Nesse caso específico, o compilador consegue saber com certeza qual o tipo de dado envolvido nas chamadas. Dessa forma podemos deixar o trabalho por conta dele. Mas existem alguns casos que não são claros:

  int i = 10;
  float f = 10.2;

  double d = soma(i,f);

------ Build started: Project: 1bit_stl, Configuration: Debug Win32 ------

Compiling...
1bit_stl.cpp
1bit_stl.cpp(115) : error C2782: 'T soma(T,T)' : template parameter 'T' is ambiguous
        1bit_stl.cpp(96) : see declaration of 'soma'
        could be 'float'
        or       'int'

Oops. Sabemos que o compilador poderia ser bonzinho e promover os dois parâmetros para double, fazer a conta, e retornar o resultado. Sim, mas lembre-se da filosofia C++: você só paga por aquilo que você pedir. Nos primeiros casos o compilador fez a dedução porque era absolutamente óbvio, nesse caso não é. Conversões implícitas podem ser uma praga a te perseguir, e o compilador C++ te livra disso exigindo que você diga exatamente o que você quer.

Outra coisa que podemos notar nesse exemplo: não existe sobrecarga de retorno de função. O fato de colocarmos o retorno da função em uma variável double não mudou em nada o comportamento da resolução de tipo. Em C++ você não pode fazer sobrecarga de função mudando somente o tipo de retorno. E esse nosso template nada mais é do que uma função vitaminada, as regras continuam valendo. Como nesse caso precisamos ser explícitos, vale a sintaxe normal:

  int i = 10;
  float f = 10.2;

  double d = soma<double>(i,f);

Dessa forma o compilador faz a promoção automática dos tipos int e float para double, o que não nos causa nenhum problema de perda de dados.

No começo do post eu falei sobre abstrair o algoritmo do tipo de dados, e é o que fizemos com nossa função soma. O conceito é simples: independente do tipo do dado, os passos necessários para se fazer uma soma são os mesmos. O que muda é a forma como a soma que é feita, que é uma característica intrínseca do tipo. Esse mesmo conceito se aplica para algoritmos mais complicados, como os de ordenação. Eles comparam os valores entre si, e a comparação de valores é diferente para cada tipo de dado. Mesmo assim, o algoritmo de ordenação continua o mesmo.

Um exemplo clássico que vou usar para ilustrar isso é uma classe para representar um número complexo. Um número complexo é representado com ai + b, sendo a e b dois números reais, e i a parte imaginária (sendo i ao quadrado igual a -1 e tendo seus detalhes explicados na Wikipedia como de costume). As operações de soma e subtração de um número complexo são feitas da seguinte forma:

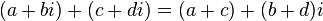
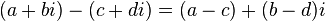
Esses algoritmos acima não se encaixam com o nosso template de soma:

  complex_number c1  = {10, 20}, c2  = {40, 30};
  soma<complex_number>(c1, c2);

------ Build started: Project: 1bit_stl, Configuration: Debug Win32 ------

Compiling...
1bit_stl.cpp
1bit_stl.cpp(98) : error C2676: binary '+' : 'complex_number' does not define this operator 
  or a conversion to a type acceptable to the predefined operator
        1bit_stl.cpp(128) : see reference to function template 
  instantiation 'T soma(T,T)' being compiled
        with
        [
            T=complex_number
        ]

Build Time 0:00
1bit_stl - 1 error(s), 0 warning(s)

---------------------- Done ----------------------

    Build: 0 succeeded, 1 failed, 0 skipped

Note que os passos para nosso complicadíssimo algoritmo ainda são os mesmos - passo único: efetuar a operação de soma - o que muda é forma como a soma é efetuada. Para ficar mais claro, imagine uma equação quadrada:

Nesse caso a soma é só um passo do algortimo para se chegar ao resultado. A forma como a soma é feita é diferente para números inteiros (int) ou reais (double), mas a ordem dessa soma dentro dos passos do algoritmo ainda é a mesma.

Voltando ao nosso super algoritmo de soma, precisamos de um tratamento diferenciado para somar números complexos. Veremos as várias formas de resolver isso no próximo post.

Em 30/05/2006 16:06, por Rodrigo Strauss

Comentários